1. ブラックボックスの限界と解釈可能性(XAI)への回帰
人工知能(AI)の歴史において、深層学習(ディープラーニング)がもたらした革命は疑いようのない事実であるが、その成功の影には常に「ブラックボックス」という不透明性が存在し続けてきた。特に、数千億のパラメータを持つニューラルネットワークは、高精度な予測を可能にする一方で、その意思決定プロセスを人間に説明することを困難にしている 1。物理学、医療、金融、法規制といった、結果の妥当性とその根拠が極めて重要視されるドメインにおいて、この不透明性は信頼性と安全性の大きな障壁となっている。こうした背景から、近年、モデル自体が人間に理解可能な数式や論理的規則で構成される「解釈可能なAI(Explainable AI, XAI)」への関心が急速に高まっており、その中核的技術としてシンボリック回帰(Symbolic Regression, SR)が再脚光を浴びている 3。
シンボリック回帰は、従来の回帰分析が特定のモデル構造(線形、多項式、指数関数など)を前提にそのパラメータのみを最適化するのに対し、データに最も適合する数式の構造そのものを探索空間から見つけ出す手法である 5。このアプローチは、データに潜む物理法則や因果関係を直接的な数学表現として抽出することを可能にし、単なる相関関係の記述を超えた「メカニズムの理解」を提供する 4。2024年から2026年にかけての最新の研究動向では、この伝統的なシンボリック回帰に大規模言語モデル(LLM)や強化学習、グラフ理論、さらには神経科学的な知見を融合させた「ニューロ・シンボリックAI」へと進化を遂げ、これまで不可能であった複雑かつ高次元な課題への適用が現実のものとなっている 8。
現代のAI研究において、人間の認知モデルはしばしば二つのシステムとして対比される。ダニエル・カーネマンの提唱した「システム1」は、高速で直感的、無意識的なパターン認識を司り、現代の深層学習の成功と重なる。一方で「システム2」は、低速で論理的、段階的かつ明示的な思考を司り、計画立案や演繹、熟考を伴う思考に対応する 10。シンボリック回帰はこのシステム2の機能をAIに付与しようとする試みであり、抽象的なシンボル(記号)の操作を通じて、自然界の摂理を数学という普遍的な言語で記述することを目指している 10。
2. シンボリック回帰の基盤理論と進化的起源
シンボリック回帰の概念的ルーツは1990年代初頭の遺伝的プログラミング(GP)に遡る。ジョン・コザらによって提案されたこの手法は、生物の進化を模倣し、数式を「表現木(Expression Tree)」として表現し、交叉や突然変異を繰り返すことで最適な解を探索するものである 3。シンボリック回帰の本質的な目標は、与えられたデータセット に対して、精度(Accuracy)と簡潔さ(Simplicity)のトレードオフを最適化する関数
を見つけ出すことにある 5。
2.1 数学表現の構造と探索空間
シンボリック回帰における探索空間は、基本演算子(,
,
,
)、基本関数(
,
,
)、入力変数、および定数の組み合わせによって構成される。これらの構成要素をノードとする木構造は、以下のような再帰的な形式で定義される 5。
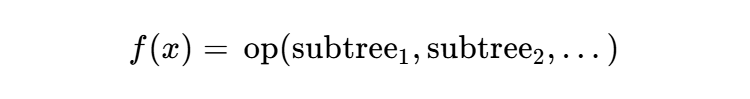
この探索問題は、数学的演算子の組み合わせが指数関数的に増大するため、本質的にNP困難な組合せ爆発を伴う 15。初期のシンボリック回帰は、主にこの巨大な離散空間を効率的に探索するためのヒューリスティクスとして進化計算を用いていた。しかし、進化計算のみでは、数式内の数値定数(係数)の微調整において限界があり、後年の勾配ベースの最適化との統合を待つこととなる 17。
2.2 伝統的アプローチの制約と現代的転換
古典的なGPベースのシンボリック回帰(例:gplearn)は、Scikit-learnスタイルのAPIを提供し、使いやすさの面で普及したが、いくつかの深刻な課題に直面していた 14。第一に、数式が世代を重ねるごとに無意味に肥大化する「ブロート(Bloat)」現象であり、これは解釈可能性を損なうだけでなく計算リソースを浪費する 20。第二に、等価な数学的表現(例: と
)を異なる個体として認識してしまうため、探索空間が不必要に冗長になる点である 7。
2020年代に入り、これらの課題を解決するために、物理的知識の注入(Physics-Informed)、深層強化学習による確率的方策、そして大規模言語モデルによる「科学的直感」の活用といった新しいパラダイムが台頭してきた 9。以下の表は、シンボリック回帰における主要なアルゴリズムの進化と、それぞれの技術的特徴をまとめたものである。
| アルゴリズムカテゴリ | 代表的な手法 | 主要なメカニズム | メ点・特徴 |
| 進化計算ベース | gplearn, DEAP, PySR | 遺伝的プログラミング、島モデル、SA | 高い並列性、多目的最適化 |
| 物理学・代数ベース | AI-Feynman, PySINDy | 単位解析、対称性チェック、スパース回帰 | 物理法則の再発見に特化 |
| 深層学習・強化学習ベース | DSR, uDSR, KAN | RNN, Transformer, 強化学習 | 勾配による最適化、高次元対応 |
| LLM統合型 | LASR, Symbolic-R1, SR-LLM | ゼロショットプロンプト、概念抽象化 | 背景知識の活用、高い探索効率 |
| グラフ・連続最適化型 | GSR, ParFam | グラフ表現、項書き換え、連続空間変換 | 数学的等価性の保持、高速収束 |
出典:7
3. 現代的シンボリック回帰のアルゴリズム的進化
2024年から2025年にかけて、シンボリック回帰は単一の最適化手法から、複数のAI技術が高度に連携するハイブリッドシステムへと進化した。特に注目すべきは、計算効率、物理的整合性、そして高次元データへの対応能力の飛躍的向上である。
3.1 PySRとSymbolicRegression.jl:高性能エンジンの確立
現在、実務家と研究者の間で最も標準的なツールとなっているのがPySRである。PySRはPythonインターフェースを持ちながら、バックエンドに高性能言語Julia(SymbolicRegression.jl)を採用している 14。この設計により、JITコンパイルやSIMD命令による数学演算の高速化、そして「島モデル(Island Model)」と呼ばれる非同期的な個体群進化を実現している 17。
PySRの特徴的な適応メカニズムの一つが、複雑性と予測損失のバランスをとるスコアリング関数である。
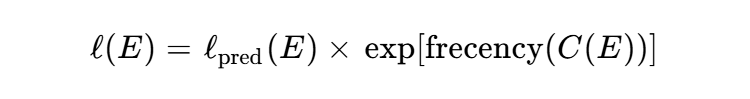
ここで、$C(E)$は表現の複雑さを示し、「フレセンシー(frecency)」スキームによって、過去に探索された単純なモデルを優先しつつ、新しい候補の探索を促す適応的なペナルティが課される 17。また、定数最適化にはBFGS法などの勾配に基づかない最適化手法が統合されており、数式の構造決定とパラメータの微調整を高度に並列化している 14。
3.2 グラフ表現と項書き換え:数学的等価性の克服
NeurIPS 2025で発表されたグラフベース・シンボリック回帰(GSR)は、従来の木構造の限界を打ち破る革新をもたらした。GSRは、数学的表現を有向非巡回グラフ(DAG)としてエンコードし、項書き換えシステム(TRS)を用いることで、代数的に等価な表現(例: と
)を単一の表現グラフ(Expression Graph)として集約する 7。この手法により、探索空間の冗長性が劇的に削減され、適合度の「報酬の希薄さ(Sparse Rewards)」が解消される。理論的解析によれば、このEG表現は一意性を持ち、探索アルゴリズム(hnMCTS)の収束性を保証している 7。
3.3 コルモゴロフ・アーノルド・ネットワーク(KAN)の衝撃
2024年に登場し、AI界に衝撃を与えたのがKolmogorov-Arnold Network(KAN)である。KANは、従来の多層パーセプトロン(MLP)がノードに固定された活性化関数を持つのに対し、エッジ上に学習可能な1変数関数(スプライン関数など)を配置する 14。これは「任意の連続関数は有限個の1変数関数の和で表現できる」というコルモゴロフ・アーノルド表現定理に基づいている 14。
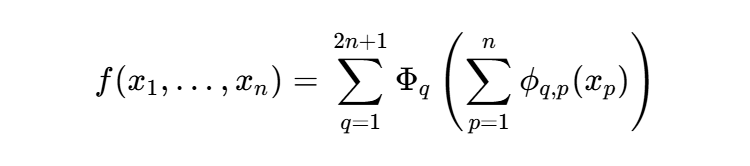
KANの利点は、学習された関数の形状をシンボリック回帰によって事後的に数式化できる点にある。これにより、深層学習のフィッティング能力を維持したまま、最終的に極めて高い解釈可能性を持つモデルを得ることが可能となる 14。
4. 大規模言語モデル(LLM)とシンボリック回帰の融合
2025年の最新の研究動向において、最も劇的なブレイクスルーをもたらしているのが、大規模言語モデル(LLM)をシンボリック回帰のコアプロセスに組み込むアプローチである。これは、AIに「数学的なセンス」と「過去の科学的知識」を付与する試みと言える 9。
4.1 LASR:概念抽象化による探索の加速
NeurIPS 2024で報告されたLASR(Latent Symbolic Regression)は、LLMを使用して成功した数式の中から「抽象的な概念」を抽出し、概念ライブラリを構築する手法である 23。 このアルゴリズムは以下の三段階のループを繰り返す。
- 概念主導の進化: LLMが過去に有効だった数学的モジュール(概念)を基に、新しい数式の候補を生成する。
- 概念の抽象化: 発見された高性能な数式パターンをLLMが分析し、再利用可能な「概念」としてライブラリに登録する。
- 概念の進化: ライブラリ内の概念自体を、LLMがより簡潔で汎用的な形式へと洗練させる。 LASRは、ファインマンの方程式群を用いたベンチマークにおいて、既存のSOTA(State-of-the-Art)手法を大きく上回る成功率を示しており、さらにはLLM自身の「スケーリング則(Scaling Laws)」の新しい形態を発見するという成果も上げている 23。
4.2 Symbolic-R1:エンドツーエンドの数式推論モデル
2026年初頭に発表されたSymbolic-R1は、シンボリック回帰タスクに特化してトレーニングされたLLMである 9。従来のLLMが数値計算や精密な数式操作に弱点を持っていたのに対し、Symbolic-R1は以下の技術によってその課題を克服した。
- Form-GRPO: 数式の「形式(Form)」の正しさとデータへの適合度を多目的に報酬とする強化学習アルゴリズム 9。
- SymbArenaデータセット: 14万件以上の多様な数式構造と、それに対応する数値データを18億トークンにわたって学習 9。
- HER(Hypothesis-Experiment-Revision): LLMがデータから仮説としての数式を立て、誤差を実験的に確認し、自己修正を行う推論サイクル 9。 Symbolic-R1は、構造的な正確さにおいて従来のPySRを凌駕し、推論コストを維持したまま数式発見の精度を飛躍的に向上させている 9。
4.3 文脈と背景知識の統合(SR-LLM)
科学的発見において、変数の「物理的な意味(単位や定義)」は探索をガイドする重要な情報である。SR-LLMフレームワークでは、検索拡張生成(RAG)を活用して、変数の物理的定義や先行研究の数式モデルをプロンプトに注入する 22。 実験結果によれば、単に数値データのみを与えるよりも、変数が「自由落下の時間」や「バネの定数」であるといった意味情報を付与することで、正しい関数形への収束が劇的に早まることが確認されている 22。これは、AIが人間のように「物理的な類推」を行いながら探索空間を絞り込んでいることを示唆している 27。
5. ベンチマークによる性能評価とアルゴリズムの比較
シンボリック回帰の進化を定量的に評価するため、コミュニティはSRBenchを中心とした標準的なベンチマーク環境を整備してきた 28。
5.1 SRBench 2.0 と「リビング・ベンチマーク」の概念
2025年にリリースされたSRBench 2.0は、130以上のデータセットを含む「生きたベンチマーク」として設計されている 28。これまでの評価指標が単なる平均二乗誤差(MSE)に偏っていたのに対し、SRBench 2.0では以下の多角的なメトリクスを導入している。
- 数式復元率(Symbolic Solution Rate): 元の数式の構造を完全に再現できた割合。
- ツリー編集距離(Tree Edit Distance, TED): 正解の数式木と予測された木構造の間の編集コスト 29。
- パレートフロント分析: 精度と複雑性のトレードオフ曲線における最適性の評価 29。
- エネルギー効率: 学習および推論にかかる電力消費量の測定(サステナブルAIの観点) 29。
5.2 主要アルゴリズムの性能比較データ
最新のベンチマーク結果によれば、PySRが依然として汎用性と数値精度のバランスで高い評価を得ているが、構造の復元においてはニューラル・シンボリック系やLLMベースのモデルが台頭している。
| アルゴリズム | 定数最適化 | 数式復元率 (%) | 精度 (R2) | 言語 | 特徴・備考 |
| PySR | BFGS / AD | 59.3 | 0.831 | Julia/Py | 科学研究のデファクト、堅牢 |
| RSRM | 勾配法 | 72.9 | 0.711 | Python | 構造復元において最高性能 |
| DSR / uDSR | 強化学習 | 43.2 | 0.755 | Python | 局所解に強く、複雑な表現に柔軟 |
| gplearn | 遺伝計算 | 16.5 | 0.728 | Python | 高速だが単純な構造に限定 |
| Symbolic-R1 | HER / RFT | 未公表 | 0.808 | LLM | LLMベース。精度と形式の統一 |
| AI-Feynman | 物理的制約 | 25.1 | 0.621 | Python | 物理法則の事前知識が不可欠 |
出典:9
特に、PySR、DEAP、gplearnをMistralやLLaMAといったLLMとペアリングした評価実験では、LLMによる「ヒント」の注入(単位情報やデータ特性の説明)が、すべてのアルゴリズムにおいて平均絶対誤差(MAE)を劇的に低下させることが示されている 26。
| アルゴリズム × LLMペア | プロンプト条件 | MAE | MSE |
| PySR × Mistral | 物理単位+構造ヒントあり | 0.010 | 0.00 |
| PySR × LLaMA | 物理単位+構造ヒントあり | 0.020 | 0.01 |
| DEAP × Mistral | 物理単位+構造ヒントあり | 0.030 | 0.01 |
| gplearn × Mistral | 物理単位+構造ヒントあり | 0.060 | 0.02 |
| PySR (単体) | ヒントなし(Baseline) | 0.150 | 0.04 |
出典:26
6. 物理学および自然科学における革新的応用
シンボリック回帰の最も直接的かつ強力なユースケースは、実験データからの物理法則の「自動再発見」および「新法則の抽出」である。従来の深層学習が物理現象を「模倣」するのに対し、シンボリック回帰は物理現象を「定式化」する 4。
6.1 高エネルギー物理学と宇宙論
大型ハドロン衝突型加速器(LHC)の実験データ解析において、標準模型を超える新しい物理学(Beyond the Standard Model)の探索にシンボリック回帰が活用されている 26。高次元のパラメータ空間において、特定の粒子の相互作用を記述する簡潔な解析的表現を見つけることは、物理学者がその理論的背景を理解するための鍵となる。 また、宇宙論においては、ハッブルの法則やケプラーの法則を観測データから直接再発見し、さらには宇宙膨張の微細な変動を記述する新しい経験式の導出にも利用されている 29。
6.2 流体力学と複雑系のモデリング
流体力学において、ナビエ・ストークス方程式の数値解法は膨大な計算コストを要する。シンボリック回帰は、高解像度シミュレーション(DNS)のデータから、より低解像度の計算格子で使用可能な「サブグリッド・スケール・モデル」を構築するために使用されている 18。 特に気候モデリングの分野では、雲の形成や海流の微細な乱れといった「サブグリッド現象」をパラメータ化するための数式を自動生成することで、地球規模の気候予測モデルの精度と解釈可能性を同時に向上させている 18。
6.3 生体組織と超弾性材料の力学
人間の脳組織などの軟組織の挙動をモデル化することは、医療機器の設計や外科シミュレーションにおいて重要である。最新の研究では、シンボリック回帰を用いて、脳組織の非線形な弾性特性を記述する「超弾性構成モデル」を自動同定している 34。 この際、物理的整合性を担保するために、以下の制約がアルゴリズムに組み込まれている。
- 多凸性(Polyconvexity): 構造的に安定な物理挙動を保証する数学的条件。
- エネルギー散逸の法則: 熱力学的な一貫性の維持。 シンボリック回帰によって得られたモデルは、複雑なニューラルネットワークモデルと同等の精度を維持しつつ、パラメータの物理的意味(剛性係数など)を直感的に把握できるという利点がある 34。
7. 材料科学および材料情報学(MI)における貢献
材料科学(マテリアルズ・インフォマティクス)において、シンボリック回帰は「記述子(Descriptor)」の発見と、物性予測の「ホワイトボックス化」を加速させている。
7.1 材料老化メカニズムの定式化
高分子材料(ゴムやプラスチック)の老化プロセスは、温度、湿度、応力といった複数の要因が複雑に絡み合っている。シンボリック回帰は、実験データからアレニウスの式を一般化した老化予測モデルを抽出することに成功している 20。 ある研究では、ゴム材料の老化挙動を記述するために、従来の経験式よりも適合度が高く、かつ物理的に解釈可能な新しい指数関数的減衰モデルを発見した 20。これは、材料の寿命予測の信頼性を高め、メンテナンスコストの削減に寄与している。
7.2 原子間ポテンシャルの開発
新材料のシミュレーションには正確な「原子間ポテンシャル(力場)」が不可欠である。従来は人間が手作業で関数形を定義していたが、シンボリック回帰を用いることで、多様な原子配置におけるエネルギー曲面を正確に記述する多体ポテンシャル関数を自動生成できる 35。 シンボリック回帰によって導出されたポテンシャルは、従来のニューラルネットワーク・ポテンシャルと比較して、外挿性能(未知の原子配置への対応力)に優れ、かつシミュレーション速度が劇的に速いという特徴がある 33。
7.3 ペロブスカイト太陽電池の安定性予測
次世代太陽電池として期待されるペロブスカイト材料において、その構造的安定性を予測する記述子の同定にシンボリック回帰が活用されている 20。 具体的には、数千種類の化合物データから、結晶構造の安定性を決定付ける幾何学的・電子的要因を組み合わせた新しい「許容因子(Tolerance Factor)」を数式として発見した。この数式は、従来の経験的な「ゴールドシュミットの許容因子」よりも高い予測精度を示し、材料探索の効率を大幅に向上させている 20。
8. 産業界における導入動向と経済的インパクト
シンボリック回帰に代表される解釈可能なAIの台頭は、学術的な枠組みを超え、企業の戦略や意思決定プロセスを根本から変えようとしている。
8.1 金融および経済予測:透明性の経済価値
金融業界において、ブラックボックスAIの使用は法規制(説明責任)の観点から制限されることが多い。シンボリック回帰は、高ノイズな金融データの中から市場の構造的関係を抽出するための有力な手段となっている 12。
- インプライド・ボラティリティ・サーフェス(IVS): オプション価格データから、市場の期待を反映するボラティリティの曲面構造を数式としてモデル化。従来のブラック・ショールズ・モデルの限界をデータ駆動で拡張している 12。
- リスク管理とスコアリング: クレジットスコアリングにおいて、なぜそのスコアになったかを明示的な数式で示すことで、融資の透明性を確保し、規制当局への説明コストを削減している 16。
8.2 製造業と予知保全:現場へのAI実装
製造現場では、熟練工の勘と経験をAIでいかに代替、あるいは強化するかが課題となっている。2026年のトレンド予測では、製造現場でのAIエージェントの採用率が40%に達するとされている 38。 シンボリック回帰は、センサーデータから機器の摩耗や故障の兆候を数式化することで、「なぜ今部品を交換すべきか」を現場のエンジニアが納得できる形で提示できる 3。これは、単なるアラートの通知を超え、運用の最適化に向けた論理的な対話を可能にする。
8.3 医療・ヘルスケア:エビデンスベースのAI
医療現場では、AIの診断根拠が医学的知見と整合していることが不可欠である。シンボリック回帰は、患者の臨床データから疾患のリスク因子を数式として抽出するために使用されている。 例えば、通院の「無断キャンセル(No-show)」のリスク予測において、患者の過去の履歴や住所、年齢などを組み合わせた簡潔な判定式をシンボリック回帰で生成し、リソースの最適配置に活用している事例がある 40。また、ウェアラブルデバイスからのリアルタイムデータに基づき、心臓病のリスクを予測する数式モデルの開発も進んでいる 11。
8.4 規制対応とガバナンス(EU AI法)
2026年までに施行される欧州AI法(EU AI Act)は、高リスクなAIシステムに対して「適切な透明性」と「説明可能性」を義務付けている 39。シンボリック回帰は、その構造自体が説明であるため、この規制要件を満たすための「Compliance-by-Design(設計によるコンプライアンス)」の代表的な解決策として注目されている。マッキンゼーの調査によれば、企業の72%がAIを導入する一方で、そのガバナンスと説明責任の欠如を最大のリスクとして挙げている 43。
9. 未解決の課題と将来の展望
シンボリック回帰は強力なツールであるが、その完全な普及にはまだいくつかの技術的・理論的障壁が存在する。
9.1 次元の呪いとスケーラビリティ
変数の数が増えると探索空間が指数関数的に増大する問題は、依然として解決の途上にある。100以上の変数を持つような高次元データセットにおいて、意味のある数式構造を短時間で発見することは困難である 24。これに対し、変数選択(Feature Selection)や、深層学習による事前圧縮、あるいはグラフベースの重複排除といった手法の統合が、2025年以降の主要な研究テーマとなっている 7。
9.2 ノイズ処理と堅牢性
現実世界のデータはノイズに満ちている。シンボリック回帰はノイズを物理的法則の一部として「過学習(Overfitting)」してしまい、複雑すぎる数式を生成する傾向がある。分位数回帰(Symbolic Quantile Regression)や、ベイズ的な事前分布を用いた正則化手法など、ノイズ耐性を高めるためのアプローチが提案されているが、標準的な手法としての確立には至っていない 12。
9.3 人間とAIの協調(Human-in-the-loop)
解釈可能性とは、単に数式が短いことだけを意味しない。それが専門家の持つ「ドメイン知識」と整合しているかが重要である。将来のシンボリック回帰システムは、人間が対話形式で数式の探索をガイドし、「この項は物理的に不自然だ」「この次元は合っていない」といったフィードバックを即座に反映できる、よりインタラクティブなものになると予測される 4。
10. 結論
シンボリック回帰(SR)に代表される「解釈可能なAI」の台頭は、人工知能の発展における一つの大きな転換点を示している。AIはこれまで、莫大なデータと計算リソースを背景に「予測の精度」を極めてきたが、今や「理解の深化」という新たなステージへと足を踏み入れている。
2024年から2026年にかけての進展は、以下の三つの次元において革命的であった。第一に、LLMとの融合により、AIが人類の数学的資産と科学的直感を活用できるようになったことである 9。第二に、グラフ理論や強化学習の導入により、複雑な物理事象を記述する方程式を、実用的な時間内でデータから直接抽出可能になったことである 7。第三に、科学から産業界に至るまで、「透明性」と「信頼性」がAI実装の必須要件となり、シンボリック回帰がその核心的技術としての地位を確立したことである 16。
シンボリック回帰は、単なる回帰分析の高度化ではない。それは、データの中に眠る自然の法則を言語化し、人間とAIが「数学」という共通言語で対話することを可能にする架け橋である。AIが導き出した簡潔な方程式を、科学者が驚きを持って眺め、そこから新たな物理的洞察を得る。そのような「AIによる科学的パラダイムの加速」こそが、シンボリック回帰が切り拓く真の未来像であると言えよう。
引用文献
- Neuro-Symbolic AI for Advanced Signal and Image Processing: A Review of Recent Trends and Future Directions, 2月 3, 2026にアクセス、 https://ieeexplore.ieee.org/iel8/6287639/10820123/11124915.pdf
- Neuro-Symbolic AI: A Foundational Analysis of the Third Wave’s Hybrid Core, 2月 3, 2026にアクセス、 https://gregrobison.medium.com/neuro-symbolic-ai-a-foundational-analysis-of-the-third-waves-hybrid-core-cc95bc69d6fa
- Symbolic Regression in Context of Machine Learning – Lark, 2月 3, 2026にアクセス、 https://www.larksuite.com/en_us/topics/ai-glossary/symbolic-regression-in-context-of-machine-learning
- From Data to Equations: Symbolic Regression as a Path to Physical AI – Fraunhofer IESE, 2月 3, 2026にアクセス、 https://www.iese.fraunhofer.de/blog/symbolic-regression-as-a-path-to-physical-ai/
- Symbolic Regression with Genetic Programming – Personal Blog, 2月 3, 2026にアクセス、 https://wildart.github.io/post/symbolicregression/
- Symbolic regression – Wikipedia, 2月 3, 2026にアクセス、 https://en.wikipedia.org/wiki/Symbolic_regression
- Graph-based Symbolic Regression with Invariance and Constraint Encoding – NeurIPS, 2月 3, 2026にアクセス、 https://neurips.cc/virtual/2025/poster/118715
- Towards Scaling Laws for Symbolic Regression – NeurIPS, 2月 3, 2026にアクセス、 https://neurips.cc/virtual/2025/131053
- FINETUNING LARGE LANGUAGE MODEL AS AN EF … – OpenReview, 2月 3, 2026にアクセス、 https://openreview.net/pdf/fd9582ca3f87537f5b3067f1ad00438dc4e17c10.pdf
- Neuro-symbolic AI – Wikipedia, 2月 3, 2026にアクセス、 https://en.wikipedia.org/wiki/Neuro-symbolic_AI
- Neuro-symbolic artificial intelligence – European Data Protection Supervisor (EDPS), 2月 3, 2026にアクセス、 https://www.edps.europa.eu/data-protection/technology-monitoring/techsonar/neuro-symbolic-artificial-intelligence_en
- The Application of Symbolic Regression on Identifying Implied Volatility Surface – MDPI, 2月 3, 2026にアクセス、 https://www.mdpi.com/2227-7390/11/9/2108
- PARFAM—(NEURAL GUIDED) SYMBOLIC REGRES- SION VIA …, 2月 3, 2026にアクセス、 https://proceedings.iclr.cc/paper_files/paper/2025/file/ca98452d4e9ecbc18c40da2aa0da8b98-Paper-Conference.pdf
- [Literature Review] Discovering equations from data: symbolic regression in dynamical systems – Moonlight, 2月 3, 2026にアクセス、 https://www.themoonlight.io/en/review/discovering-equations-from-data-symbolic-regression-in-dynamical-systems
- AI Feynman: A physics-inspired method for symbolic regression – PMC, 2月 3, 2026にアクセス、 https://pmc.ncbi.nlm.nih.gov/articles/PMC7159912/
- Contemporary Symbolic Regression Methods and their Relative Performance | Request PDF – ResearchGate, 2月 3, 2026にアクセス、 https://www.researchgate.net/publication/380424072_Contemporary_Symbolic_Regression_Methods_and_their_Relative_Performance
- PySR: Symbolic Regression for Scientific Discovery – Emergent Mind, 2月 3, 2026にアクセス、 https://www.emergentmind.com/topics/pysr-method
- Introduction to Equation Discovery – Comparing Symbolic Regression Methods, 2月 3, 2026にアクセス、 https://m2lines.github.io/L96_demo/notebooks/symbolic_methods_comparison.html
- Find Hidden Laws Within Your Data with Symbolic Regression, 2月 3, 2026にアクセス、 https://towardsdatascience.com/find-hidden-laws-within-your-data-with-symbolic-regression-ebe55c1a4922/
- Symbolic regression accelerates the discovery of quantitative relationships in rubber material aging – OAE Publishing Inc., 2月 3, 2026にアクセス、 https://www.oaepublish.com/articles/jmi.2024.103
- LLM-Meta-SR: In-Context Learning for Evolving Selection Operators in Symbolic Regression, 2月 3, 2026にアクセス、 https://arxiv.org/html/2505.18602v2
- SR-LLM: An incremental symbolic regression framework driven by LLM-based retrieval-augmented generation – PMC, 2月 3, 2026にアクセス、 https://pmc.ncbi.nlm.nih.gov/articles/PMC12772181/
- Symbolic Regression with a Learned Concept Library – NIPS, 2月 3, 2026にアクセス、 https://proceedings.neurips.cc/paper_files/paper/2024/file/4ec3ddc465c6d650c9c419fb91f1c00a-Paper-Conference.pdf
- Recent Advances in Symbolic Regression | CoLab, 2月 3, 2026にアクセス、 https://colab.ws/articles/10.1145%2F3735634
- Symbolic Regression with a Learned Concept Library, 2月 3, 2026にアクセス、 https://arxiv.org/abs/2409.09359
- Knowledge integration for physics-informed symbolic regression …, 2月 3, 2026にアクセス、 https://pmc.ncbi.nlm.nih.gov/articles/PMC12800073/
- MOBLLM: Model Building LLMs via Symbolic Regression and Experimental Design – DSpace@MIT, 2月 3, 2026にアクセス、 https://dspace.mit.edu/bitstream/handle/1721.1/162509/binbas-bbinbas-meng-eecs-2025-thesis.pdf?sequence=1&isAllowed=y
- SRBench: Symbolic Regression Benchmarks – Cava Lab, 2月 3, 2026にアクセス、 http://cavalab.org/symbolic-regression/
- Symbolic Regression Benchmarks – Emergent Mind, 2月 3, 2026にアクセス、 https://www.emergentmind.com/topics/symbolic-regression-benchmarks
- Call for Action: Towards the Next Generation of Symbolic Regression Benchmark – arXiv, 2月 3, 2026にアクセス、 https://arxiv.org/html/2505.03977v1
- GeoBench: A new benchmark on Symbolic Regression with Geometric Expressions, 2月 3, 2026にアクセス、 https://openreview.net/forum?id=TqzNI4v9DT
- LLM-SRBench: A New Benchmark for Scientific Equation Discovery with Large Language Models | OpenReview, 2月 3, 2026にアクセス、 https://openreview.net/forum?id=SyQPiZJVWY
- Symbolic regression in the physical sciences | Royal Society, 2月 3, 2026にアクセス、 https://royalsociety.org/science-events-and-lectures/2025/04/symbolic-regression/
- Automated data-driven discovery of material models based on symbolic regression: A case study on the human brain cortex – PMC, 2月 3, 2026にアクセス、 https://pmc.ncbi.nlm.nih.gov/articles/PMC12205916/
- Artificial Intelligence in Physical Sciences: Symbolic Regression …, 2月 3, 2026にアクセス、 https://pmc.ncbi.nlm.nih.gov/articles/PMC10113133/
- [1901.04136] Symbolic Regression in Materials Science – arXiv, 2月 3, 2026にアクセス、 https://arxiv.org/abs/1901.04136
- Symbolic Quantile Regression for the Interpretable Prediction of Conditional Quantiles – arXiv, 2月 3, 2026にアクセス、 https://arxiv.org/html/2508.08080v1
- 2026 Manufacturing Industry Trends and Predictions – IFS Blog, 2月 3, 2026にアクセス、 https://blog.ifs.com/2026-manufacturing-industry-trends-and-predictions/
- AI in 2026: Predictions, Trends & Industry Forecast – Digital Marketing Agency, 2月 3, 2026にアクセス、 https://www.digitalapplied.com/blog/ai-predictions-2026-trends-forecast
- Decision analysis framework for predicting no-shows to appointments using machine learning algorithms – PMC – PubMed Central, 2月 3, 2026にアクセス、 https://pmc.ncbi.nlm.nih.gov/articles/PMC10770919/
- 22 MIT startups to watch in 2025, 2月 3, 2026にアクセス、 https://mitsloan.mit.edu/ideas-made-to-matter/22-mit-startups-to-watch-2025
- ILNAS white paper « Artificial Intelligence – Portail-Qualité.lu, 2月 3, 2026にアクセス、 https://portail-qualite.public.lu/dam-assets/publications/normalisation/2021/ilnas-white-paper-artificial-intelligence.pdf
- AI stats every business must know in 2026 – Intuition, 2月 3, 2026にアクセス、 https://www.intuition.com/ai-stats-every-business-must-know-in-2026/
- SRBench++ : principled benchmarking of symbolic regression with domain-expert interpretation – PMC – NIH, 2月 3, 2026にアクセス、 https://pmc.ncbi.nlm.nih.gov/articles/PMC12321164/

