現代の産業界において、人工知能(AI)の活用は単なる効率化の手段を超え、企業の存立を左右する戦略的基盤となっている。しかし、現在のAI開発の主流であるディープラーニングをはじめとした結合主義的アプローチは、その予測精度の高さと引き換えに、判断プロセスの不透明性という致命的な課題を抱えている。特に高い説明責任が求められる法規制下のビジネスや、物理現象の理解が不可欠な製造・材料科学の現場では、この「ブラックボックス問題」がAIの社会実装を阻む大きな障壁となっている 1。この課題に対する根源的な解決策として、ジェラルド・ナドラーと日比野省三が提唱した「ブレイクスルー思考」の設計哲学と、データから明示的な数式を導き出す「シンボリック回帰(記号回帰)」の技術を統合する、新たな目的志向型AI活用モデルが浮上している。本報告書では、これら二つのパラダイムがどのように共鳴し、従来のデカルト的分析手法を超越した、創造的かつ説明可能なビジネスソリューションを構築し得るかを詳述する。
ブレイクスルー思考の哲学的転換:デカルト的パラダイムからの脱却
ジェラルド・ナドラーと日比野省三によって提唱された「ブレイクスルー思考」は、400年来の伝統を持つデカルト的な分析的思考、すなわち「問題を細分化し、過去のデータを徹底的に調査して原因を特定し、それを修正する」というアプローチを根底から覆すものである 3。この従来の分析手法は、既存のシステムを修理する(Repair)ことには適しているが、真に新しい価値を創造する(Design)ことには適していない 3。
設計アプローチと分析アプローチの対比
デカルト的な思考様式は、現象を部分に分解し、因果関係を過去に遡って解明しようとする。しかし、複雑な相互作用を持つ現代のビジネスシステムにおいて、過去のデータに固執することは、しばしば「分析による麻痺(Analysis Paralysis)」を引き起こし、競合他社の後塵を拝する結果を招く 3。これに対し、ブレイクスルー思考は「システム・ビュー」、すなわち有機的、目的志向的、かつ全体論的な視点に基づいている 3。このパラダイムでは、現在の問題を直視する前に、まず達成すべき理想の未来(次々世代解)を設計し、そこから逆算して現在の行動を決定する 3。
| 特徴 | デカルト的分析アプローチ | ブレイクスルー思考(設計アプローチ) |
| 思考の方向 | 過去から現在(なぜ起きたか) | 未来から現在(何を目指すか) |
| 主な目的 | 原因の特定と問題の修正 | 理想の解決策の設計 |
| 情報の扱い | 網羅的・徹底的なデータ収集 | 目的達成に必要な最小限の情報 |
| システム観 | 要素還元主義(分解と合成) | ホリスティック(全体論・有機的) |
| 創造性 | 既存の枠内での改善 | 既存の枠を超えた革新(ブレイクスルー) |
この表が示すように、ブレイクスルー思考への転換は、単なる手法の変更ではなく、ビジネスの目的そのものを再定義するプロセスである。過去の成功例や競合他社の数値をベンチマークとするのではなく、理論上の限界や絶対的な目標(例:コストゼロ、欠陥ゼロ)をターゲットとする「絶対ベンチマーク」の考え方が、その核心にある 3。
ブレイクスルー思考を支える7つの原則
ブレイクスルー思考の実践は、従来の常識とは異なる7つの原則( assumption)に基づいている 3。これらは、AIシステムが単なる「過去のパターンの模倣」に陥るのを防ぎ、真にユニークなビジネス解を導くためのガイドラインとなる。
- ユニークネスの原則(Uniqueness Principle): 全ての課題は独自のものであり、他社の成功事例をそのままコピーしても解決にはならない。その状況特有の人間、時間、場所の要因を考慮した「状況特定解(Situation Specific Solution: 3S)」を追求すべきである 3。
- 目的の原則(Purposes Principle): 「何が悪いか」を問うのではなく、「何のためにこれを行うのか」という目的を問い直し、それを階層的に拡大していく。これにより、本質的な課題を明確にし、不要な作業を排除できる 3。
- 次々世代解の原則(Solution-After-Next Principle): 目先の解決策ではなく、理想的な将来像を先に設計する。たとえ現在は実現不可能であっても、その理想像をターゲットとして持つことで、現在の意思決定に方向性が与えられる 4。
- システムの原則(Systems Principle): あらゆる問題はより大きなシステムの一部であり、解決策が他の部分にどのような影響を及ぼすかを全体的に把握する必要がある。システム全体としての整合性を重視する 3。
- 限定的情報収集の原則(Limited Information Collection Principle): 過度なデータ収集は創造性を阻害し、問題を固定化させる。解決策を構想するために本当に必要な情報だけを、目的主導で収集する 3。
- 参加の原則(People Design Principle): 解決策のユーザーや影響を受ける人々を設計プロセスの初期から関与させる。これにより、人間の知恵(ホット・インフォメーション)を活用し、導入時の抵抗を最小化できる 3。
- 継続的改善の原則(Betterment Timeline Principle): 完成した解決策も、環境の変化に合わせて常に更新されなければならない。時間軸に沿った改善プログラムを最初から組み込んでおく 3。
目的拡大法:システムの全体像を捉える手法
ブレイクスルー思考において最も強力なツールの一つが「目的拡大法(Purpose Expansion)」である。これは「チャイニーズ・ボックス(マトリョーシカ)」のようなシステムの階層構造を前提としている 3。ある活動の目的を問い(目的1)、さらに「その目的の目的は何か」と問い続けることで(目的2、目的3…)、より抽象度が高く、かつ本質的な「究極の目的」へと到達する 3。
例えば、トヨタの創業者である豊田喜一郎は、フォードのベルトコンベアをそのまま導入するのではなく、その目的を「部品を動かすこと」から「効率的な生産の流れを作ること」へと拡大し、さらに「必要な時に必要なものを運ぶ」という本質的な目的に到達した 3。この目的の深掘りこそが、トヨタ生産方式という独自のシステムを生み出す原動力となった。AIビジネスにおいても、この手法を適用することで、アルゴリズムが目指すべき「評価関数」を、単なるエラー最小化から、企業の長期的戦略目標へと昇華させることが可能となる。
シンボリック回帰の技術的パラダイム:数式による透明性の確保
シンボリック回帰(SR)は、観測されたデータセットに最も適合する数学的表現(数式)を探索し、自動的に発見する機械学習手法である 6。一般的な線形回帰や多項式回帰が、あらかじめ決められた関数の形(モデル構造)の中で係数のみを調整するのに対し、シンボリック回帰は関数の形そのものを探索空間とし、演算子(,
,
,
,
,
など)を組み合わせて最適なモデルを構築する 6。
ホワイトボックスAIとしてのシンボリック回帰
現在のAIブームを牽引するディープラーニングは、膨大なパラメータを持つニューラルネットワークを通じて高い予測精度を実現するが、その内部構造は人間には理解不能なブラックボックスである 6。一方、シンボリック回帰の出力はコンパクトな物理学や数学の公式と同じ形式の「数式」である。これにより、モデルがどのような理屈で予測を行っているのかを人間が直接確認し、既存のドメイン知識と照らし合わせることが可能になる 6。
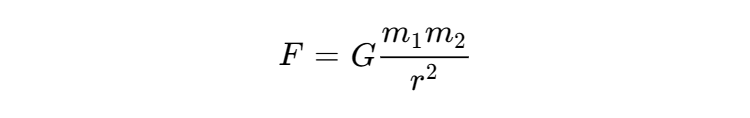
例えば、ニュートンの万有引力の法則のような構造を、データから直接導き出すことができる。ニューラルネットワークが「計算機」として答えを出すのに対し、シンボリック回帰は「科学者」として法則そのものを提示すると表現される 6。
アルゴリズムと探索手法の多様性
シンボリック回帰の実装には、いくつかの主要なアプローチが存在する。
- 遺伝的プログラミング(Genetic Programming: GP): 最も伝統的な手法であり、数式を木構造として表現し、交叉(一部の入れ替え)や突然変異(一部の変更)を繰り返しながら、データへの適合度と式の簡潔さを両立する個体を「進化」させる 6。
- SINDy(Sparse Identification of Nonlinear Dynamics): 物理システムの動力学に特化した手法で、あらかじめ用意された膨大な関数のライブラリ(多項式、三角関数など)の中から、スパース回帰を用いてシステムを記述する最小限の項を選択する 11。探索空間を制限することで計算効率を劇的に向上させている。
- ディープ・シンボリック回帰(DSR): 強化学習やリカレントニューラルネットワーク(RNN)を用いて、数式の記号列を生成するアプローチである。ニューラルネットワークの柔軟な学習能力とシンボリックな出力の解釈性を統合している 8。
- AI Feynman: 物理データの性質(対称性、加法分離性など)を利用して探索空間を分割し、複雑な物理法則を効率的に発見するために設計されたシステムである 6。
| 手法 | メカニズム | 主な利点 | 課題 |
| 遺伝的プログラミング | 数式の木構造を進化させる | 柔軟性が高く、事前知識なしで機能 | 計算コストが高く、過学習の懸念 |
| SINDy | 関数のライブラリから選択 | 高速、物理法則の同定に強い | 適切なライブラリの設計が必要 |
| ディープ・シンボリック回帰 | 強化学習による記号生成 | 大規模データへの適応性 | 学習プロセスのチューニングが困難 |
| AI Feynman | 物理的対称性の利用 | 物理法則の発見に極めて強力 | 物理法則以外の汎用データへの適用 |
少数データに対する頑健性と汎化性能
ニューラルネットワークが性能を発揮するためには膨大な教師データが必要だが、シンボリック回帰は、真の物理的・数学的構造を見つけ出すことができれば、非常に少数のデータポイントからでも正確な予測モデルを構築できる 6。これは、モデルがデータの背後にある「普遍的なルール」を抽出しているためであり、学習データの範囲外を予測する「外挿性能」においても、ブラックボックスモデルより優れていることが多い 9。
ブレイクスルー思考とシンボリック回帰の統合シナリオ
ナドラーのブレイクスルー思考(BT)とシンボリック回帰(SR)を統合することで、ビジネスにおけるAI活用は「データ主導の予測」から「目的主導の法則発見」へと進化する。BTが「何のために、何を達成すべきか」という戦略的枠組みを提供し、SRがその枠組みの中で「どのような物理的・論理的関係性が存在するのか」という具体的な知識を明示化する。
目的(Purposes)を評価関数(Fitness Function)へ変換する
シンボリック回帰の探索において、最も重要なのは「何をもって最適な数式とするか」という評価基準(フィットネス関数)の設計である。通常、これは二乗平均平方根誤差(RMSE)のような統計的な指標に限定される。しかし、ブレイクスルー思考の「目的の原則」を適用すれば、評価基準に戦略的な重みを加えることができる 3。
例えば、ある化学プラントの反応効率を最適化する場合、単に収率を予測するだけでなく、「副産物の排出を最小化する」「エネルギー消費を抑える」といった上位の目的を評価関数に組み込む。SRは、これらの多面的な目的を同時に満たす、最も「美しく(簡潔で)かつ戦略にかなった」数式を探索空間から見つけ出す。これは、BTが提唱する「全体システム」の最適化を、数学的な制約条件としてAIに組み込む行為に等しい 5。
「次々世代解」としての理想的な数式構造
BTの「次々世代解の原則」は、SRにおける「事前知識の統合」として機能する。エンジニアやドメインエキスパートが、理想的なシステムが従うべき物理法則(例:エネルギー保存則、対称性)をあらかじめ定義し、SRの探索をその「理想の形」の周辺に集中させる 3。
これにより、AIは単に現状のデータを説明するだけでなく、理想的な状態に向けた「あるべき関係性」を数式として提示する。もし、現状のデータが理想の数式から大きく乖離している場合、それはシステムに改善の余地があることを示唆する「ブレイクスルーの種」となる 3。
限定的情報収集による「思考の生産性」向上
ナドラーは「情報の集めすぎは創造性を殺す」と説いた 5。SRも同様に、入力変数が多すぎると探索空間が指数関数的に増大し、計算不能に陥る(NP困難問題) 18。 ここでBTの「限定的情報収集の原則」を適用することで、SRの効率を劇的に高めることができる。目的拡大法を通じて特定された「本質的な変数」のみをSRに投入することで、AIはより短時間で、かつ解釈性の高いモデルを発見できるようになる。これは「データの量」ではなく「目的の質」によってAIの性能を引き出すという、新しいデータサイエンスの形である 3。
産業界における実践的応用ケーススタディ
BTとSRの統合モデルは、特に製造、材料科学、サプライチェーン、金融といった「説明可能性」と「物理的妥当性」が重視される分野で真価を発揮する。
ケース1:製造業における高効率制御と予測保守
シーメンス(Siemens)などの先進的なメーカーでは、複雑な製造プロセスを制御するためにSRを活用している。従来のモデル予測制御(MPC)はCPUへの負荷が高く、標準的なプログラマブル・ロジック・コントローラ(PLC)でリアルタイムに実行することが困難であった 18。 ここにSRを適用することで、MPCの動作を近似する「簡潔な数式ルール」を自動抽出できる。このルールは軽量でPLC上でも高速に動作し、かつ人間が論理を検証できるため、現場のオペレーターが自信を持ってAIの判断を採用できる(参加の原則) 18。また、BTの「システムの原則」に従い、個別の機械だけでなく工場全体のエネルギー消費を最適化する目的をSRに反映させることで、局所最適を避けた全体最適が実現される 5。
ケース2:材料開発(マテリアルズ・インフォマティクス)における新法則発見
材料科学の分野では、新材料の特性(強度、弾性、伝導性など)と、その組成や製造条件の間の複雑な関係を解明することが最大の課題である。SRは、この未知の関係性を数式として明示化する強力なツールとなる 21。 例えば、ゴム材料の劣化プロセスの研究では、SRを用いてミクロな化学構造の変化とマクロな物理的強度の相関を数式化した事例がある 23。この数式により、研究者は「なぜこの温度で劣化が加速するのか」というメカニズムを物理的に理解し、BTの「次々世代解」に基づいた、より耐久性の高い理想的な材料設計へとつなげることが可能になった 22。
| 産業分野 | 従来のAI(ブラックボックス)の限界 | BT+SR統合による解決 |
| 製造・設備 | 故障予測の根拠が不明で、メンテナンスの判断が困難 | 摩耗の物理的メカニズムを数式化し、説明可能な予兆検知を実現 |
| 材料開発 | 高精度な物性予測はできるが、新材料の設計指針が立たない | 特性を支配する支配方程式を発見し、理想の材料設計を支援 |
| 金融・リスク管理 | ローン審査の拒絶理由が説明できず、透明性に欠ける | 審査基準を人間が読める数式として定義し、法規制への適合を確保 |
| サプライチェーン | 需要予測の変動に弱く、在庫の過不足が発生しやすい | 在庫変動の因果関係を明示化し、戦略目的に沿った意思決定を支援 |
ケース3:金融と意思決定心理学における時間選好の同定
経済学や心理学における「時間割引(delay discounting)」の研究、つまり「将来の報酬より現在の報酬を好む」人間の行動傾向を解明する際にも、SRは有効である 14。 AI Feynmanを用いた実験では、被験者の行動データから、現在最も正確とされる「双曲割引モデル」の数式構造を自動的に再発見することに成功した 14。BTの「ユニークネスの原則」に基づき、特定の顧客セグメントごとに異なる時間割引の数式を同定することで、より個別化された、かつ論理的根拠のある金融商品の提案が可能になる 3。
AIエンジニアリングと組織的ガバナンスへの影響
BTとSRの統合は、技術的な側面だけでなく、AIを開発・管理する組織のあり方にも変革を迫る。
DIKWPモデルを通じた知の階層化
この統合アプローチを組織的に実装するためのフレームワークとして「DIKWPモデル」が有効である。これは、データ(Data)、情報(Information)、知識(Knowledge)、知恵(Wisdom)、目的(Purpose)の5つの層からなる認知モデルである 16。
- データ・情報層: 現場のセンサーやERPから収集された生の事実。
- 知識層: シンボリック回帰によって発見された「普遍的な数式・法則」。
- 知恵・目的層: ブレイクスルー思考によって定義された「戦略的目標」と、その法則をどう社会やビジネスに適用するかという「人間的判断」 16。
このモデルでは、最上位の「目的」が最下位の「データ収集」を規定するという動的なループが形成される。AIエンジニアは単に精度を競うのではなく、組織の「目的」をいかにAIの「知識(数式)」に翻訳するかという、より高度な役割を担うことになる 16。
検証可能性ファースト(Verifiability-First)のエンジニアリング
AIが社会の基盤となる「AIware」の時代において、最大のボトルネックはAIの生成する振る舞いの検証である 24。ニューラルネットワークの出力をテストケースで検証するのは困難だが、シンボリック回帰が出力する数式は、既存の数学的・物理的整合性チェックや、フォーマルメソッドによる検証が容易である 24。 BTの「継続的改善の原則」に従い、環境の変化によって数式が妥当性を失った場合に即座に検知し、モデルを自動的に再構築するパイプラインを構築することが、次世代のAIガバナンスの標準となる 5。
結論と今後の展望
ジェラルド・ナドラーと日比野省三が示した「ブレイクスルー思考」の哲学は、AIがもたらす不透明性と決定論的な未来予測という閉塞感を打破するための、極めて強力な羅針盤である。そして「シンボリック回帰」という技術は、その哲学を数学的な厳密さと計算機パワーによって具体化するための最良のエンジンである。
この二つの統合による「目的志向型AIビジネス」は、以下の三つの価値を同時にもたらす。
- 信頼の構築: ブラックボックスを排除し、誰もが理解・検証可能な数式として知を明示化することで、ステークホルダーからの信頼を獲得する。
- 創造性の解放: 過去のデータの延長線上ではない「次々世代解」をAIに探索させることで、人間単独では到達できなかったイノベーションを誘発する。
- 戦略的機敏性: 目的の階層構造をAIに組み込むことで、市場環境や経営戦略の変化に迅速かつ論理的に適応する組織能力を実現する。
今後の展望として、大規模言語モデル(LLM)とシンボリック回帰を組み合わせた「神経記号的AI(Neuro-Symbolic AI)」の進化が期待される。LLMが持つ膨大なテキスト知識を「目的の抽出」や「目的拡大法」のプロセスに活用し、その目的の下でSRが物理的な法則を特定するというハイブリッドな形態が、将来のビジネスAIの主流となろう 26。
AIはもはや、人間を代替する自動化ツールではなく、人間の「目的」を数学的な「法則」へと翻訳し、理想の未来を共に設計するための共創パートナーとなる。ナドラーと日比野が提唱した「ブレイクスルー」の精神をAIの中に宿すことこそが、真に豊かなデジタル社会を築く鍵である。
引用文献
- What is Explainable AI (XAI)? – IBM, 2月 13, 2026にアクセス、 https://www.ibm.com/think/topics/explainable-ai
- Why businesses need explainable AI—and how to deliver it – McKinsey, 2月 13, 2026にアクセス、 https://www.mckinsey.com/capabilities/quantumblack/our-insights/why-businesses-need-explainable-ai-and-how-to-deliver-it
- ÿþM i c r o s o f t W o r d – 0 3 I 0 3 e P 2 H i b i n o 0 6 0 7 3 1 . d o c, 2月 13, 2026にアクセス、 https://www.osaka-gu.ac.jp/php/nakagawa/TRIZ/eTRIZ/elinksref/eJapanTRIZ-CB/e2ndTRIZSymp06/eKeynotes06/eHibinoPaper060731.pdf
- Breakthrough Thinking: A Systems Concept for Creative Strategic …, 2月 13, 2026にアクセス、 https://globalioc.com/wp-content/uploads/2018/11/Breakthrough-Thinking-Overview.pdf
- Seven Principles of Creative Problem Solving | PDF – Scribd, 2月 13, 2026にアクセス、 https://www.scribd.com/document/492865078/Seven-Principles-of-Creative-Problem-Solving
- Power of Symbolic Regression. Symbolic regression is a form of …, 2月 13, 2026にアクセス、 https://medium.com/@manamnathtiwari/power-of-symnolic-regression-a18eef139f64
- From Data to Equations: Symbolic Regression as a Path to Physical AI – Fraunhofer IESE, 2月 13, 2026にアクセス、 https://www.iese.fraunhofer.de/blog/symbolic-regression-as-a-path-to-physical-ai/
- Knowledge Integration for Physics-informed Symbolic Regression Using Pre-trained Large Language Models, 2月 13, 2026にアクセス、 http://www.diva-portal.org/smash/get/diva2:1968832/FULLTEXT01.pdf
- Symbolic regression outperforms other models for small data sets – ar5iv – arXiv, 2月 13, 2026にアクセス、 https://ar5iv.labs.arxiv.org/html/2103.15147
- A Unified Data-Driven Framework for Efficient Scientific Discovery – arXiv, 2月 13, 2026にアクセス、 https://arxiv.org/html/2509.07303v1
- ADAM-SINDy: An Efficient Optimization Framework for Parameterized Nonlinear Dynamical System Identification – arXiv, 2月 13, 2026にアクセス、 https://arxiv.org/html/2410.16528v1
- The illustration of the SINDy-PI algorithm on Michaelis-Menten… – ResearchGate, 2月 13, 2026にアクセス、 https://www.researchgate.net/figure/The-illustration-of-the-SINDy-PI-algorithm-on-Michaelis-Menten-dynamics-a-The_fig1_346113263
- (PDF) Interpretable scientific discovery with symbolic regression: a review – ResearchGate, 2月 13, 2026にアクセス、 https://www.researchgate.net/publication/377080608_Interpretable_scientific_discovery_with_symbolic_regression_a_review
- Application of the symbolic regression program AI-Feynman to psychology – Frontiers, 2月 13, 2026にアクセス、 https://www.frontiersin.org/journals/artificial-intelligence/articles/10.3389/frai.2023.1039438/full
- POM’s Expanding Constellation – Production and Operations Management Society, 2月 13, 2026にアクセス、 https://www.poms.org/archive/conferences/Meeting2004/POMS_CD/Browse%20This%20CD/PAPERS/Program.pdf
- (PDF) Semantic Analysis and Improvement Suggestions for the AI-Newton System Based on the Networked DIKWP×DIKWP Model – ResearchGate, 2月 13, 2026にアクセス、 https://www.researchgate.net/publication/398869533_Semantic_Analysis_and_Improvement_Suggestions_for_the_AI-Newton_System_Based_on_the_Networked_DIKWPDIKWP_Model
- Responsible Artificial Intelligence for Earth Observation – IEEE Xplore, 2月 13, 2026にアクセス、 https://ieeexplore.ieee.org/iel8/6245518/11177000/10897919.pdf
- Symbolic Regression with AI – Siemens Global, 2月 13, 2026にアクセス、 https://www.siemens.com/global/en/company/stories/research-technologies/artificial-intelligence/symbolic-regression.html
- AI in the Sciences and Engineering Symbolic Regression and Model Discovery, 2月 13, 2026にアクセス、 https://ethz.ch/content/dam/ethz/special-interest/math/applied-mathematics/camlab-dam/documents/AISE2024/AISE24%2024%20Symbolic%20Regression%20and%20Model%20Discovery.pdf
- Why Explainable AI Is Becoming Essential for Manufacturing Execution – LeanDNA, 2月 13, 2026にアクセス、 https://www.leandna.com/resource/explainable-ai-for-manufacturing-execution/
- Symbolic regression in the physical sciences | Royal Society, 2月 13, 2026にアクセス、 https://royalsociety.org/science-events-and-lectures/2025/04/symbolic-regression/
- Symbolic regression in materials science | MRS Communications | Cambridge Core, 2月 13, 2026にアクセス、 https://www.cambridge.org/core/journals/mrs-communications/article/symbolic-regression-in-materials-science/A5836F4AF5E9395A9B27541C5042A7F3
- Symbolic regression accelerates the discovery of quantitative relationships in rubber material aging – OAE Publishing Inc., 2月 13, 2026にアクセス、 https://www.oaepublish.com/articles/jmi.2024.103
- (PDF) Verifiability-First AI Engineering in the Era of AIware: A Conceptual Framework, Design Principles, and Architectural Patterns for Scalable Verification – ResearchGate, 2月 13, 2026にアクセス、 https://www.researchgate.net/publication/399520173_Verifiability-First_AI_Engineering_in_the_Era_of_AIware_A_Conceptual_Framework_Design_Principles_and_Architectural_Patterns_for_Scalable_Verification
- Neuro-symbolic AI and knowledge engineering | School of Computer Science and Informatics | University of Liverpool, 2月 13, 2026にアクセス、 https://www.liverpool.ac.uk/computer-science-and-informatics/research/artificial-intelligence/neuro-symolic-ai-knowlege-engineering/
- Neuro-symbolic artificial intelligence | European Data Protection Supervisor, 2月 13, 2026にアクセス、 https://www.edps.europa.eu/data-protection/technology-monitoring/techsonar/neuro-symbolic-artificial-intelligence_en
- Unlocking the Potential of Generative AI through Neuro-Symbolic Architectures – Benefits and Limitations – arXiv, 2月 13, 2026にアクセス、 https://arxiv.org/html/2502.11269v1

